Homotecia 

La Homotecia

una transformación geométrica plana, en la cual los puntos relacionados o transformados se denominan homotéticos, y cumplen las siguientes condiciones:

Los puntos homotéticos están alineados con un tercero fijo llamado centro de la Homotecia (O).

La relación entre los segmentos definidos por este centro y los puntos transformado y original es una constante denominada razón de la homotecia (k).

                   Ejemplo#1

Ejemplo#2 

Ejemplo#3

       Deslizamiento:

       Un deslizamiento se define como un movimiento de una masa de roca, detritos o tierra pendiente abajo bajo la acción de la gravedad, cuando el esfuerzo de corte excede el esfuerzo de resistencia del material.

      La palabra deslizamiento proviene del verbo deslizar. Hay dos teorías sobre el origen etimológico de esta palabra. Una es que esta palabra proviene de una raíz onomatopéyica -liz-. La otra teoría es que esta palabra deriva del prefijo –des–  y izar,  este último es un elemento compositivo que viene del latín, usado para crear verbos. El latín culto usó izar con Z porque se parece más al sonido griego original.

   

ejemplo#1

ejemplo#2

DEFINICIONES: Gráfica tridimensional.

   Gráfica tridimensional.

DEFINICIONES:

tener 9 o 10 dimensiones. En física, geometría y análisis

matemático, un objeto o ente es tridimensional si tiene tres dimensiones. Es decir cada uno de sus puntos puede ser localizado especificando tres números dentro de un cierto rango. Por ejemplo, anchura, longitud y profundidad.

El espacio a nuestro alrededor es tridimensional a simple vista, pero en realidad hay más dimensiones, por lo que también puede ser considerado un espacio tetra-dimensional si incluimos el tiempo como cuarta dimensión. La teoría de Kaluza-Klein original postulaba un espacio-tiempo de cinco dimensiones, la teoría de cuerdas retoma esa idea y postula  según diferentes
versiones que el espacio físico podría 

                 Ejemplo #1                                                                             

  

                                                                                          














Ejemplo#2

              Ejemplo#3                                                                                                             
                            

                                      

                                                      

             Rotación:

     Rotación es la acción de rotar, girar, dar vuelta.  Se le llama rotación al movimiento que hace la tierra sobre su propio eje (llamado eje rotatorio) el cual está inclinado 23°, 27, es un eje imaginario basado en la eclíptica (que es la línea por la que el sol hace un movimiento aparente, visto desde la tierra). La rotación es uno de los cuatro movimientos que realiza la tierra, junto con los movimientos de traslación, nutación y precesión.

En matemática, las rotaciones son transformaciones lineales que son isométricas, es decir,que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interior y cuya matriz tiene la propiedad de ser ortogonal

Ejemplo:1

Ejemplo:2

   

  

Ovalo Dado el Eje Mayor y Eje menor.

  Ovalo Dado el Eje Mayor  y Eje menor.

Construir un óvalo conociendo su eje menor.

Los extremos del eje menor dado serán centros de dos de los cuatro arcos de este óvalo (O3 y O4) y cuyo radio será igual al propio eje menor. Trazamos una circunferencia auxiliar de diámetro igual al eje menor dado que cortará a su mediatriz en los puntos O2 y O1, centros de los dos arcos restantes. Los puntos de enlace se calculan uniendo centros y con ellos los radios de los arcos de centros O1 y O2, arcos que cortarán a la mediatriz del eje menor en A y B, extremos del eje mayor.

  

Ovoide:

Construir un ovoide conociendo su eje.

Dado el eje AB lo dividimos en seis partes iguales siendo las partes 2ª y 5ª los centros O1 y O2 de la semicircunferencia y arco desigual. Con centro en la 2ª división y radio 2B, trazamos un arco que corta en O3 y O4, centros de los arcos iguales, a la prolongación del diámetro. El radio de la semicircunferencia es O1-A y sus extremos T1 y T2 puntos de enlace. El radio del arco desigual de centro O2 es O2-B. Para determinar los puntos de enlace T4 y T3 unimos O4 y O3 con O2 cortando en su prolongación al arco trazado con centro en O2. Los radios de los arcos iguales son O4-T4 o O3-T3.

SIMETRIA AXIAL:

Simetría, un concepto que deriva del latín symmetrĭa, hace referencia a la correspondencia que se registra entre la posición, la forma y el tamaño de los componentes de un todo. Axial, por su parte, es aquello vinculado a un eje (la pieza que actúa como sostén de algo y que, en ciertos contextos, permite que un determinado objeto gire) Se conoce como simetría axial a la simetría que existe en torno a un eje cuando la totalidad de los semiplanos que se toman desde una determinada mediatriz exhiben las mismas características.

Trazado de Curvas Técnicas:

Trazado de Curvas Técnicas:

Concepto de curva técnica

Son curvas de aplicación en la ingeniería y en la arquitectura.

Óvalos y ovoides

Son curvas técnicas formadas por circunferencias tangentes entre sí: con forma de huevo (ovoides) o con forma parecida a la de las elipses (óvalos).

En la figura vemos un óvalo inscrito en un 

Espirales, volutas y evolventes

Son curvas técnicas, engendradas por un punto que se aleja o se acerca a su origen según se mueva en uno u otro sentido. Algunas están formadas por arcos de circunferencia (como las espirales de centros alineados, las de centros en los vértices de polígonos, regulares o no, las volutas y las espirales áurea y logarítmica). Otras espirales son representaciones de trayectorias, como la espiral de Arquímedes y la evolvente de la circunferencia.

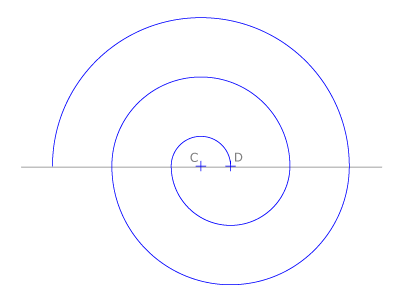
En la figura vemos la espiral más sencilla, la de Honnecourt, con dos centros

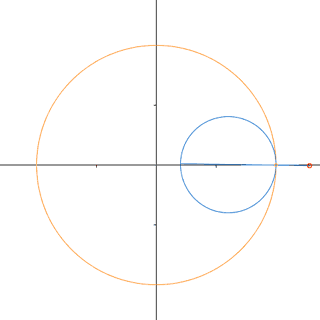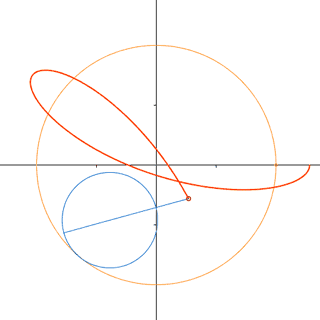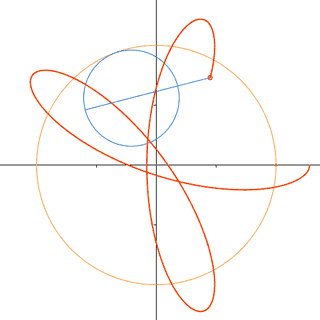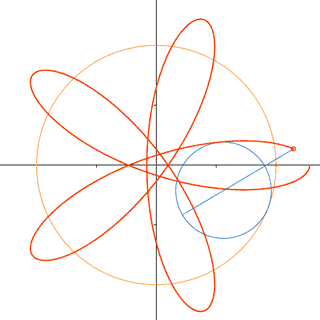
Curvas cíclicas

Son representaciones de trayectorias que se repiten una vez cumplido su ciclo. Por ejemplo, la cicloide es la trayectoria de un punto fijo sobre una circunferencia que se desplaza en línea recta, recorriendo espacios iguales en tiempos iguales.

 curvas

La hélice cilíndrica, que no es una curva plana, también se estudia por ser de gran aplicación en arquitectura (escaleras de caracol) en ingeniería (formas helicoidales).